
Institut für elegante Mathematik ... gruppe eM
Int'l Conference on Real Analysis and Measure Theory »CARTEMI«
Ischia, Italy, 2004
"Application of Quasitopoi, Galois Connections, 16 years after ..."
Rolf D. Brandt, BEB, Hannover, Germany
eM Institute, "located world wide" (L'Aquila, Hannover, Montpellier, Toledo, ...)
abstract:
For practical purposes it is really one of the most efficient ways to construct limits (and colimits) via simple liftings of limits (colimits) of atoms for the corresponding universal structure. Applying these techniques is nothing else than just practising the real kernel of Topoi, Galois Theory, and other universal constructions.Lifting of Galois Connections is applying atoms in Galois Theory. We will give examples for industrial applications with regard to topological editors and topological navigation techniques, optimisers, pattern recognition, forecasters, chasing correspondences in data universes, data and referential integrity, and time series.
Working with "measures" means in this sense use of "continuous accumulations" instead of values for individual intervals, working "analytically" corresponds to universal principles, e.g. partial morphisms, cartesian closedness, limits and so on instead of methods from numerical analysis.
The "spirit of topological structures in the sense of Alexander Grothendieck" helps nowadays even with constructing models for theoretical physics as well as computer science.
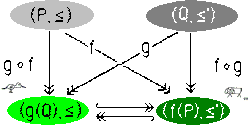
→ pdf-file of talk: "Application of Quasitopoi, Galois Connections, 16 years after ..."
Ref.:
→ "Quasitopoi for Analysis", Capri, 1988, »CARTEMI«
→ "Quasitopoi for Topology", Sorrento, 1988
→ "Topos theoretical principles in optimization", Vienna, 1990
→ "Hereditary Topological Categories and Applications to Classes of Convergence Spaces", Baku, 1987
→ - " - , Conference Proceedings, Baku, 1989 (→ pdf-file)
→ "Applications of Quasitopos Axioms in Optimisation", Antwerp, 1998
→ Strutture Generali di Convergenza per Filtri, Connessioni di Galois e "Atomi" per Strutture Iniziali, L'Aquila, 1987
→ - " - , pdf-version Quaderni matematici, Trieste, 1987

»CARTEMI« 2004
July 12-16, 2004, Ischia, Italy
####### 1st quote from topology-news@atlas-conferences.com: Topology News, December 2003 ###########
Eleventh Meeting on Real Analysis and Measure Theory
11-17 July, 2004Ischia, Italy
Since 1984 the meeting on Real Analysis and Measure Theory has been a biannual event of European relevance where established scientists and young researchers discuss their recent work in fundamental mathematical disciplines such as measure theory, real analysis, lattice theory, taking into consideration their role in applications to decision theory, economics, mathematical finance and theoretical physics. The meeting is also an occasion for discussing new developments, unexpected relations with other mathematical fields, and new connections with applications. With a program of scientific talks of reasonable density, we wish to fix the state of the art in the topics the meeting covers and, simultaneously, to give young scientists a concrete occasion to start/test their research in cooperation with world-famous specialists.
The Meeting is successfully organized every two years. The present edition will be held in Ischia (NA) in the period 11-17 July, 2004. The site of the meeting will be Hotel Continental Terme.
As usual, there will be 50 minutes invited lectures (we still are defining the program) and shorter communications (25 minutes, we think).
As for the previous occasions, papers presented at CARTEMI can be published in the journal Atti del Seminario Matematico e Fisico dell'Universita' di Modena following the usual "rules" of any publication (papers must be of original content, are referred....) and they normally appear on several issues of the journal. Only finally, all the papers will be collected to form the volume of Proccedings.
Scientific Committee
V. Aversa, C.D. Aliprantis, A. Basile, A. Bella, B. Bongiorno,
D. Candeloro, P. de Lucia, E. De Pascale, G. Di Maio, L. Paganoni,
E. Pap, P. Ptak, A. Volcic, H. Weber, J.D.M. Wright.
Organizing Committee
P. de Lucia, A. Basile, E. D'Aniello, A. De Simone, C. Tarantino.
At the end of January we will send the registration form and the reservation form for the hotel.
 ####### 1st unquote ###########
last update December 19, 2003
####### 1st unquote ###########
last update December 19, 2003
further info → www.ams.org/mathcal/info/2004_jul11-17_ischia.html,
conference info: → www.dma.unina.it/~cartemi/.
 Scheduled
Scheduled ![]() talk:
talk:
"Application of Quasitopoi, Galois Connections, 16 years after ..." (abstract see above).
≥15 years old stuff:
→ abstract "Quasitopoi for Analysis", Capri, 1988, »CARTEMI«
→ abstract "Quasitopoi for Topology", Sorrento, 1988
→ abstract "Topos theoretical principles in optimization", Vienna, 1990
→ abstract "Hereditary Topological Categories and Applications to Classes of Convergence Spaces", Baku, 1987
 → paper - " -, Baku, 1989
(→ pdf-file).
→ paper - " -, Baku, 1989
(→ pdf-file).
summary 1998:
→ summary "Applications of Quasitopos Axioms in Optimisation", Antwerp, 1998
####### last update January 5, 2004 #######
Measure Theory
Volume 4: Topological Measure
by D.H.Fremlin, University of Essexhttp://www.essex.ac.uk/maths/staff/fremlin/mtcont.htm
Contents
* Chapter 41: Topologies and measures I
* Chapter 42: Descriptive set theory
* Chapter 43: Topologies and measures II
* Chapter 44: Topological groups
* Chapter 45: Perfect measures and disintegrations
* Chapter 46: Pointwise compact sets of measurable functions
* Chapter 47: Geometric measure theory
* Chapter 48: Gauge integrals
* Chapter 49: Further topics
Appendix
For prices and how to order, see
http://www.essex.ac.uk/maths/staff/fremlin/mtsales.htm
####### 2nd unquote ########### last update December 19, 2003
φφ
Info to group eM: Institute for elegant Mathematics
https://www.algrotopoi.de/group eM is a world-wide active net of engineers, mathematicians, and other researchers. We are open to anybody to help solving problems and/or to find potential experts.